Product added to cart
- Inicio
- Blog
- Libus Comunidad
- Nivel de protección en auditivos

En el boletín técnico de noviembre mencioné que los índices de atenuación son dependientes de un parámetro de naturaleza estadística denominado nivel de protección. Este parámetro debe interpretarse como el porcentaje de usuarios a los que se les asegura la mínima protección especificada por el índice que caracteriza al protector auditivo en cuestión.
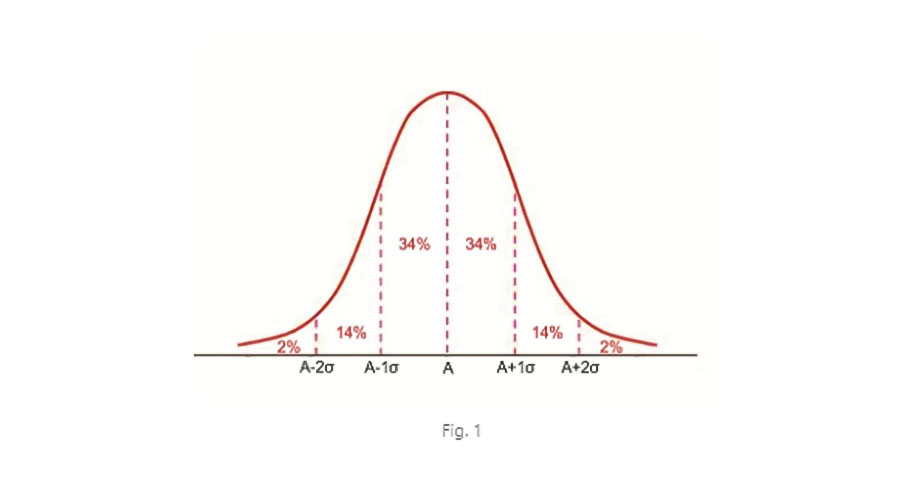
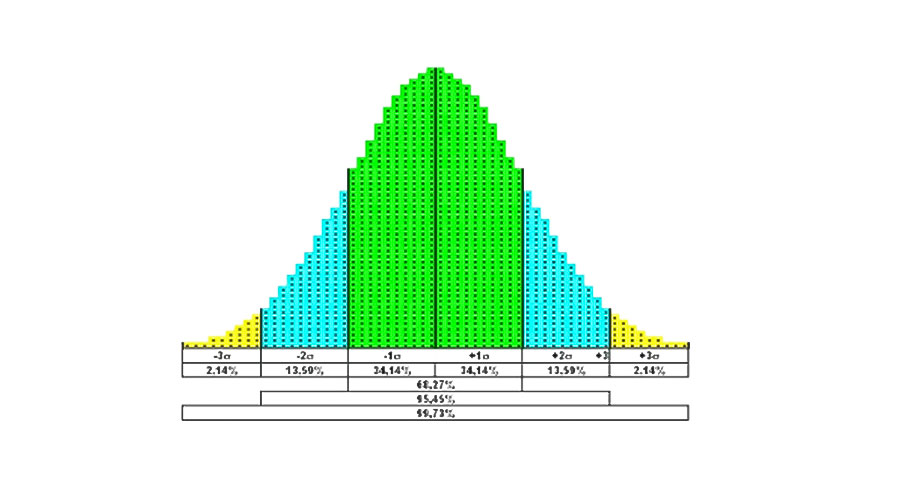
La mayoría de los procesos naturales responden a una distribución de probabilidad denominada normal o gaussiana (ver Anexo). La atenuación de un protector auditivo en uso también. Si consideramos un protector con una atenuación promedio A y una desviación estándar σ, la gráfica de su función de densidad de probabilidad es como la de la figura de la derecha. Por las propiedades de una distribución normal sabemos que entre ± 1σ se encuentra el 68% de la población y entre ± 2σ el 96% (34+14+34+14) como se ve en la fig. 1. El resto de la población (4%) se encuentra desde ± 2σ hasta el infinito. Obviamente, la suma de todos los porcentajes da 100%, el total de la población.
Si tomamos un lote de fabricación de este protector auditivo con atenuación promedio A podemos decir con certeza que sólo el 50% de los usuarios estará protegido por esa atenuación o más, ya que es la población que, estadísticamente, se encuentran por encima del valor promedio (A+1σ, A+2σ, etc.) como muestra la fig. 2.
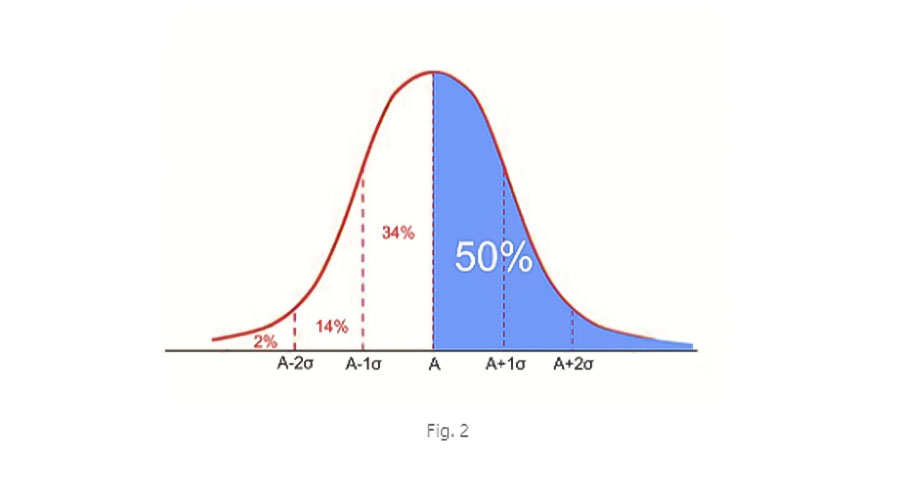
Si queremos garantizar un nivel de protección a mayor cantidad de individuos debemos asumir un margen de seguridad demeritando la atenuación promedio.
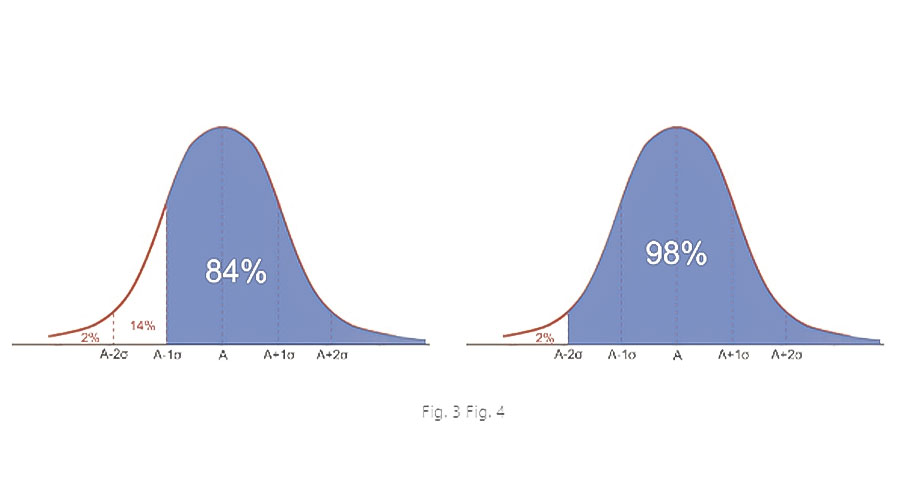
Si restamos 1σ a la atenuación promedio podemos decir que el protector
brindará una atenuación de, al menos, A-1σ (
Restando 2σ aseguramos una atenuación mínima de A-2σ al 98% de los usuarios
que utilicen correctamente el protector (fig. 4).
Como vimos en el boletín de noviembre, en el cálculo del NRR se restan 2
desviaciones estándar, es decir, tiene en cuenta al 98% de los usuarios.
El NRRsf resta 1 desviación estándar por lo que incluye al 84% de los
usuarios.
El SNR está formulado para ser calculado para diferentes niveles de
protección (si bien 84% es el habitual). A mayor nivel deseado mayor será el
número de desviaciones estándar que tendremos que restar al valor medio de
atenuación en cada octava; llamando α al multiplicador y siendo α * σ el
valor a restar:
Anexo - Conceptos de Probabilidad y Estadística y distribución normal
- Ing. Adrián Balonga / Jefe de Laboratorio de LIBUS S.A.
Al análisis de los eventos gobernados por la probabilidad se le llama
estadística. La estadística es una herramienta indispensable para la toma de
decisiones. Evaluar la probabilidad de un evento es simplemente intentar
determinar a priori que tan frecuentemente se producirá. Dada su naturaleza
aleatoria, el futuro siempre es incierto. Cuando no existe certeza del
resultado de un evento, podemos hablar de la probabilidad de ciertos
resultados dependiendo de qué tan frecuentemente ocurren y sobre ese
conocimiento histórico hacer presunciones. En la década de 1560, Gerolamo
Cardano escribe el primer tratado serio sobre probabilidad.
Pierre Laplace sentó las bases de la teoría analítica de la probabilidad.
Fue el primero que planteó que, dado un resultado cualquiera x,
dentro de un conjunto finito de N resultados posibles, donde ninguno
tiene más oportunidades de darse que otro, la probabilidad de que ocurra
x es:
Estadística: es la rama de las matemáticas relacionada con el estudio
de fenómenos aleatorios cuyo resultado es imprevisible con certeza y con la
forma de tomar decisiones razonables basadas en observaciones previas de
dichos fenómenos.
Población: en estadística, es un conjunto de resultados, sucesos,
sujetos, elementos, individuos, objetos o fenómenos que presentan
características comunes que se desean estudiar.
Histograma: en estadística, es una representación gráfica de una
variable en forma de barras, donde la altura de cada barra es proporcional a
la frecuencia de repetición de los valores en ciertos rangos.
Supongamos que soy fabricante de platos y estos deben tener un determinado
peso objetivo. Para determinar con qué tolerancia en el peso puedo
comprometerme a fabricarlos, mido este parámetro con una balanza para cada
uno de platos del lote. Hecho ésto, los ordeno en pilas alrededor del peso
promedio; podría tener una distribución de platos como la que se ve en la
imagen.
Lo que vemos es el histograma del peso de los platos fabricados; es una
"primera vista" de la distribución de la población.
La distribución normal fue presentada por Abraham de Moivre en un artículo
del año 1733. El nombre de Gauss se ha asociado a esta distribución porque
la usó con profusión cuando analizaba datos astronómicos. La distribución
normal, habitualmente llamada “Campana de Gauss”, tiene una gran importancia
en muchísimas ramas de la ciencia porque permite caracterizar numerosos
fenómenos naturales, sociales y psicológicos.
La mayoría de los fenómenos que se cuantifican con una variable continua
como las dimensiones (peso, altura, intensidad, etc) siguen una distribución
normal. La distribución normal es la más extendida por lo que muchos ensayos
estadísticos están basados en una "normalidad" más o menos justificada de la
variable aleatoria bajo estudio.
Para familiarizarse con la distribución gaussiana es interesante observar
una “máquina de Galton”; en ella se dejan caer una gran cantidad de bolillas
(que representan a cada individuo de una población) que van encontrando
obstáculos en su caída (que representan a fuentes de variación o dispersión)
que las obligan a desviarse de su trayectoria con probabilidad 50% a
izquierda o derecha (https://www.youtube.com/watch?v=8AD7b7_HNak)
Sólo 2 parámetros caracterizan a la distribución normal:
el promedio [m]: se calcula como la media aritmética de los datos y
corresponde al centro de la campana.
la desviación estándar [σ]: se calcula como la raíz cuadrada del
promedio de la diferencia de cada valor con el promedio elevada al cuadrado
y es una medida relativa del ancho de la campana.
Pero lo más útil que nos informa es cómo se distribuye la población (área
bajo la curva):
Toda vez que nos encontremos frente a la incertidumbre respecto de una
medida o de un fenómeno natural de características continuas (se puede medir
en una escala graduada) y no tenemos información respecto de su
distribución, asumir que se distribuye según la normal es la mejor opción. Y
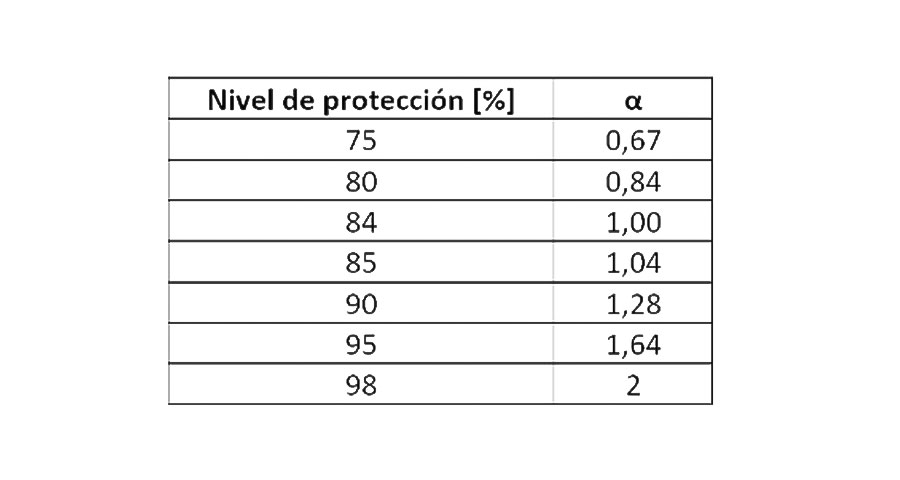
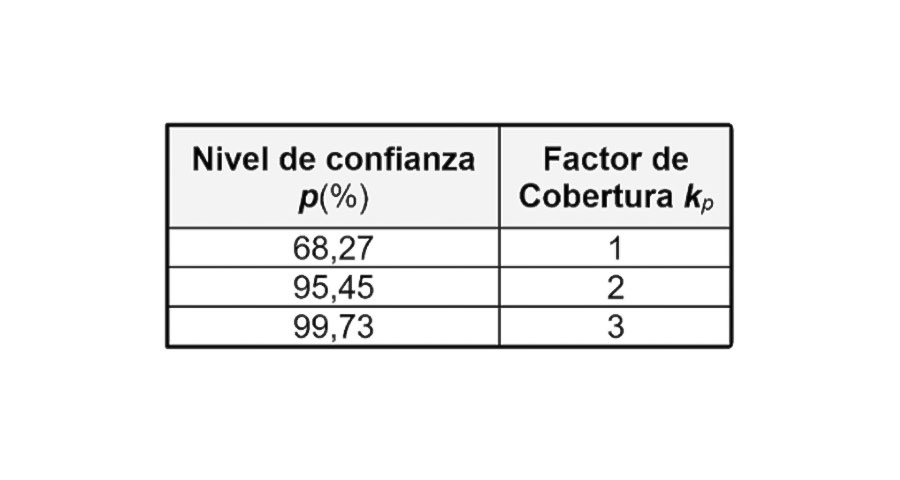
si debemos dar un índice de confianza respecto de un valor medido, es
habitual que se tome un factor de cobertura dado en términos de desviaciones
estándar tal como se muestra en la tabla.
Libus, es una empresa argentina que desde hace 20 años viene diseñando y
fabricando elementos de protección personal para la cabeza, con materiales
de gran calidad y confort. Tiene su planta modelo en Berazategui,
Provincia de Buenos Aires, con un moderno laboratorio de ensayo y medición
para testear productos que poseen todas las certificaciones nacionales e
internacionales necesarias para su comercialización y uso.
Probabilidad y Estadística
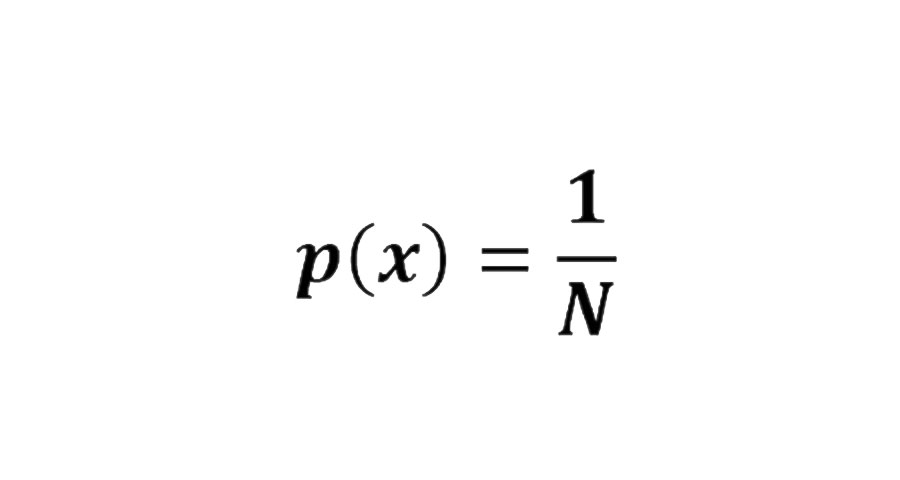

Distribución Normal o Gaussiana (Campana de Gauss)
Acerca de Libus
Categorias
- Tips de seguridad personal (1)
- Libus Comunidad (9)
- Libus Service (1)
- Protección Respiratoria (9)
- Protección Craneana (2)
- Workshop (0)
- Eventos (0)
- PROTEÇÃO RESPIRATÓRIA (0)
- LIBUS COMUNIDADE (0)
Mensajes recientes
Archivo
Etiquetas



 LAT
LAT







